Формула аннуитета. Вечная рента. Это надо знать каждому! (не для банкиров)
 В современном мире, где банковские продукты входят в жизнь любого человека, понимание сути финансовой математики и умение делать простые финансовые вычисления становится необходимым навыком. Но многие учебники и статьи по этой теме написаны сложным языком финансовых терминов и математических формул. Без терминов и формул, конечно, не обойтись. Однако объяснить суть вычислений можно простым языком, понятным любому человеку. Эта статья — продолжение статьи о дисконтировании денежных потоков. В ней речь пойдет об аннуитете (аннуитетных денежных потоках). Вечная рента, формула аннуитета — расчет текущей и будущей стоимости на простых примерах, объяснения для людей, а не для банкиров – об этом вы узнаете, прочитав данную статью.
В современном мире, где банковские продукты входят в жизнь любого человека, понимание сути финансовой математики и умение делать простые финансовые вычисления становится необходимым навыком. Но многие учебники и статьи по этой теме написаны сложным языком финансовых терминов и математических формул. Без терминов и формул, конечно, не обойтись. Однако объяснить суть вычислений можно простым языком, понятным любому человеку. Эта статья — продолжение статьи о дисконтировании денежных потоков. В ней речь пойдет об аннуитете (аннуитетных денежных потоках). Вечная рента, формула аннуитета — расчет текущей и будущей стоимости на простых примерах, объяснения для людей, а не для банкиров – об этом вы узнаете, прочитав данную статью.

Что такое аннуитет?
Услышав слово аннуитет, многие подумают о чем-то сверхсложном и недоступном для понимания. На самом деле всё просто, только слово иностранное.
Аннуитет – это серия одинаковых платежей через одинаковые промежутки времени. Этот термин представляет собой буквенный «перевод» английского слова annuity, что означает «fixed sum paid every year». Люди, владеющие английским языком, вспомнят еще слово «annual», которое в переводе означает «годовой». Оба этих слова происходят от латинского слова annuus – ежегодно. Таким образом, в самом слове аннуитет содержится указание на ежегодную периодичность платежей.
На временной линии (или шкале времени) аннуитетные денежные потоки можно изобразить, например, вот так (Рис. 1):
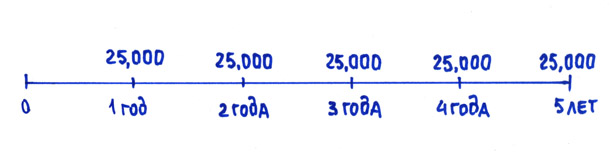
В настоящее же время аннуитетом называются не только серии одинаковых годовых платежей, но и любые последовательности одинаковых по сумме платежей вне зависимости от их периодичности. Это могут быть ежегодные, ежеквартальные, ежемесячные платежи. Главным остаётся одно: аннуитет – это несколько одинаковых платежей (денежных потоков) через одинаковые промежутки времени. Например, зарплата. Если ваша зарплата постоянна в течение года, то ежемесячный приток денежных средств в виде зарплаты является аннуитетом с ежемесячным периодом выплаты. Другой пример: если вы покупаете какую-то вещь в рассрочку, то ваши ежемесячные платежи банку тоже будут аннуитетом.
Пренумерандо и постнумерандо
Еще немного терминов. Аннуитеты бывают пренумерандо и постнумерандо. Это красивые и загадочные термины обозначают всего лишь момент платежа: пренумерандо означает платежи в начале каждого временного периода, постнумерандо — в конце его. Эти термины, пришедшие к нам, судя по всему из латыни, используются в учебниках или в официальных бумагах. Я же буду говорить по-русски: денежные потоки с выплатой в конце года или в начале года.
В данной статье рассматриваются примеры расчета простых аннуитетов, в которых период платежа и период начисления процентов равны друг другу. То есть если проценты начисляются, например, за год, то и выплаты будут ежегодными. Или проценты начисляются ежемесячно, и платежи тоже осуществляются ежемесячно. Существуют аннуитеты, в которых эти периоды не совпадают (периоды выплат и периоды начисления процентов), но это более сложные вычисления. Я не буду их затрагивать. Всем, кто хочет разобрать эту тему досконально, лучше обращаться к учебникам по финансовой математике.
Дисконтирование и наращение
Для начала вспомним о том, что такое дисконтирование и наращение. Более подробно об этом рассказано в предыдущей статье. В ней речь шла о дисконтировании и наращении единичного денежного потока, то есть одной денежной суммы. Продисконтировать – это значит рассчитать текущую стоимость будущего денежного потока. То есть, если вам надо накопить определенную сумму к какой-то дате в будущем, то, применив дисконтирование, вы сможете рассчитать, сколько надо положить в банк сегодня.
Наращение – это движение из сегодняшнего дня в завтрашний: расчет будущей стоимости тех денег, которые у вас есть сегодня. Если вы положите деньги на банковский счет, то, зная банковскую ставку, вы сможете рассчитать, сколько денег у вас накопится на счете в любой момент времени в будущем.
Наращение и дисконтирование, конечно, неприменимы, если вы храните деньги дома. Все эти расчеты справедливы только тогда, когда вы можете инвестировать ваши деньги: положить на банковский счет или купить долговые ценные бумаги.
Дисконтирование и наращение применяются не только к одному денежному потоку, но и к последовательности денежных потоков, при этом денежные суммы могут быть любыми по величине. Частным случаем таких множественных денежных потоков и являются аннуитеты.
Формула аннуитета
Аннуитетные денежные потоки тоже можно дисконтировать и наращивать, то есть определять их текущую и будущую стоимости.
Например, это необходимо, когда нам нужно выбрать между двумя предлагаемых нам вариантами получения денег. Не зная основных положений финансовой математики, можно прогадать и выбрать заведомо невыгодный для себя вариант. Чем и пользуются более осведомленные участники финансового рынка, а именно банки.
Расчет аннуитета — дисконтирование
ПРИМЕР 1. Возьмем абстрактный пример. Допустим, вам надо выбрать, что лучше:
- (А) получить 100,000 долларов сегодня или
- (Б) 5 раз по 25,000 долларов в конце каждого из следующих 5 лет.
В сумме 5 * 25,000 = 125,000, что вроде бы лучше, чем 100,000 долларов. Но так ли это? Ведь у денег есть еще и «временная» стоимость. Банковская ставка в данный момент в данной стране, допустим, равна 10%.
Вариант (Б) представляет собой простой вариант аннуитета. Только не все знают, что это именно так называется. Чтобы сравнить эти два варианта между собой (что выгоднее?), надо привести их к одному моменту времени, поскольку стоимость денег в разные моменты времени различна. В данном случае надо продисконтировать аннутитетный денежный поток (Б), т.е. рассчитать его сегодняшнюю стоимость. Если дисконтированная стоимость аннуитета будет больше, чем 100,000 долларов, значит, второй вариант выгоднее при данной ставке процента.
В предыдущей статье мы научились дисконтировать одиночную сумму. Те же вычисления можно сделать и в этот раз, только придется повторить их 5 раз.
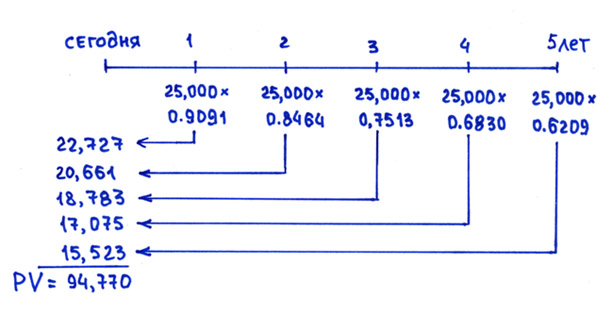
На данной шкале времени кроме платежа в сумме 25,000 нанесены соответствующие каждому периоду коэффициенты дисконтирования. Таблица коэффициентов дисконтирования приведена в предыдущей статье про дисконтирование.
Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая табличка:
- 25,000*0,9091 = 22,727
- 25,000*0,8264 = 20,661
- 25,000*0,7513 = 18,783
- 25,000*0,6830 = 17,075
- 25,000*0,6209 = 15,523
- Итого: 94,770
Здесь сумма платежа умножена на соответствующий каждому году коэффициент дисконтирования. В целом пять платежей по 25,000 в конце каждого года с учетом дисконтирования стоят 94,770, что несколько меньше, чем 100,000 сегодня. Следовательно, 100,000 сегодня при ставке 10% будет выгоднее, чем предложенный аннуитет 5 лет по 25,000.
Этот пример важен не только, чтобы еще раз продемонстрировать временную стоимость денег. Из таблицы становится ясно, как можно упростить вычисление дисконтированной стоимости аннуитета. Вместо того чтобы дисконтировать каждую сумму отдельно, можно сложить все коэффициенты дисконтирования и умножить только один раз:
25,000*(0,9091+0,8264+0,7513+0,6830+0,6209) что аналогично 25,000*3,7908=94,770
Из этого примера легко вывести математическую формулу расчета дисконтированной стоимости аннуитета.
Сначала вспомним, как выглядит формула дисконтирования:
PV = FV*1/(1+R)n
Коэффициент дисконтирования равен 1/(1+R)n — это 0,9091, 0,8264 и т.д. в нашем примере.
Формула аннуитета (для расчета дисконтированной стоимости аннуитетных денежных потоков)
PV = FV*[1/(1+R)1 + 1/(1+R)2 + 1/(1+R)3 + 1/(1+R)4 +1/(1+R)5]
И так далее, в зависимости от того, сколько у вас периодов времени.
Выражение в квадратных скобках можно представить математически, но вряд ли это нужно большинству людей. Это называется коэффициент аннуитета, или аннуитетный коэффициент дисконтирования, точное название не столь важно. В примере выше этот коэффициент равен 3,7908.
Гораздо полезнее уметь пользоваться таблицами таких коэффициентов для расчета приведенной (дисконтированной) стоимости аннуитетного денежного потока. Такие таблицы позволяют быстро решать простые задачи на дисконтирование аннуитетов. Пример такой таблицы дисконтирования приведен ниже:
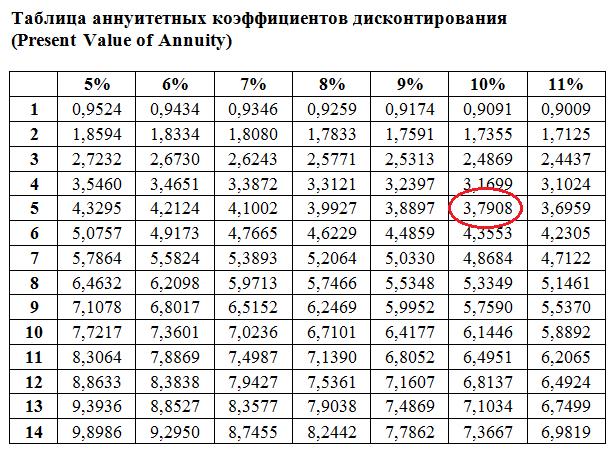 Если кому-то нужна точная формула аннуитета, точнее формула коэффициента дисконтирования аннуитета, то вот она:
Если кому-то нужна точная формула аннуитета, точнее формула коэффициента дисконтирования аннуитета, то вот она:
Коэффициент дисконтирования аннуитета: 1/R — 1/(R*(1+R)n)
Дисконтированная стоимость аннуитета: PV= платеж умножить на коэффициент
Расчет аннуитета — наращение
В примере выше мы считали дисконтированную стоимость денежного потока. То есть приводили стоимость денежного потока к текущему моменту времени. Можно решать и обратную задачу – узнать будущую стоимость аннуитета (аннуитетного денежного потока).
ПРИМЕР 2. В нашем первом примере мы можем посчитать будущую стоимость обоих вариантов. Если перевести из области чистой математики в жизненную плоскость, то надо выбрать, что лучше:
- (А) положить сегодня 100,000 долларов в банк под 10% годовых или
- (Б) в конце каждого года делать взносы в сумме 25,000.
Для первого варианта можно воспользоваться таблицей коэффициентов наращения (она есть в предыдущей статье).
Для варианта (А) будущая стоимость считается просто: $100,000 через 5 лет будут равны 100,000*1,6105 = $161,050
Для варианта (Б) ситуация несколько сложнее.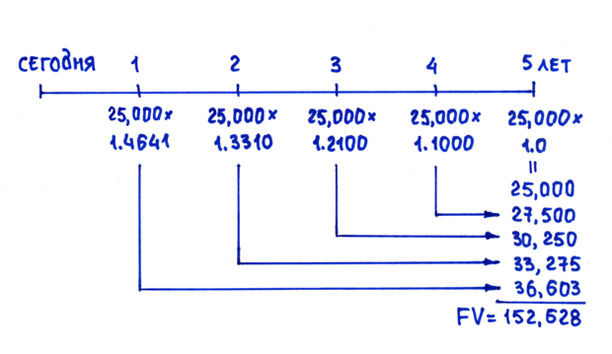
Мы хотим узнать, сколько будет у нас на счете через 5 лет, если мы будем откладывать 25,000 в конце каждого года. То есть мы сделаем последний взнос и сразу же посчитаем, сколько мы накопили. Чтобы не ошибиться, лучше подписать коэффициенты наращения, соответствующие каждому году, на шкалу времени. Первый платеж будет сделан в конце первого года, это значит, что через 5 лет по нему будут наращены проценты только за 4 года. Соответственно, по второму платежу мы получим проценты за 3 года, по третьему – за два года, по четвертому – за один год, и, наконец, положив деньги в пятый раз, проценты по последнему взносу еще нее возникнут (то есть надо будет умножить на 1,10 в нулевой степени!)
25,000*(1,1) 4+25,000*(1,1)3 + 25,000*(1,10)2 + 25,000*(1,10)1 + 25,000 (1,10)0 что равно
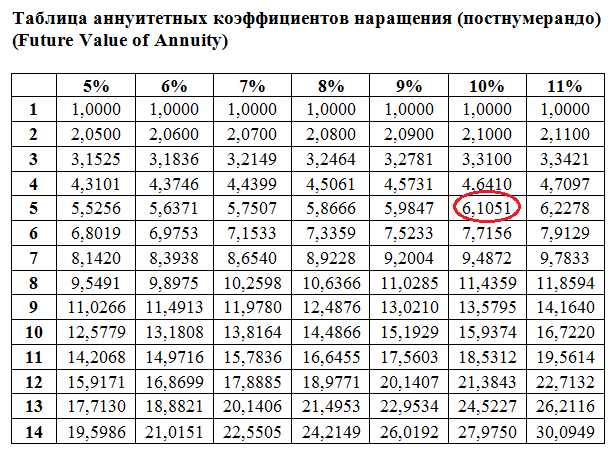
25,000*1,4641 + 25,000*1,3310 +25,000*1,2100 +25,000*1,1000 + 25,000*1 = 25,000*6,1051 = 152,628
Будущая стоимость аннуитета (вариант Б) равняется $152,628, что существенно меньше, чем $161,050 (вариант А). Это означает, что выгоднее внести на банковский счет 100,000 долларов сегодня, чем делать взносы 25,000 в конце каждого из 5 следующих лет. Данный вывод справедлив для банковской ставки 10% годовых.
Для расчета будущей стоимости аннуитетных денежных потоков тоже имеются таблицы коэффициентов. В данном случае этой таблицей можно пользоваться для расчета аннуитетов с платежами в конце временного интервала (т.е. постнумерандо).
 Для любителей математики формула аннуитета для расчета его будущей стоимости выглядит так:
Для любителей математики формула аннуитета для расчета его будущей стоимости выглядит так:
Коэффициент наращения аннуитета: FV = платеж умножить на коэффициент,
где коэффициент равен: [(1+R)n – 1]/R
Это был аннуитет с платежами в конце каждого года (постнумерандо).
ПРИМЕР 3.Можно рассмотреть и другой пример. Сколько мы накопим на счете в банке, если будем вносить по 25,000 в начале каждого года, а не в конце? Это будет так называемый аннуитет пренумерандо, назовем его вариант В. Этот денежный поток можно изобразить на шкале времени таким образом:

Как видно из рисунка, платежи по 25,000 делаются в начале каждого годового периода. Например, вы решили класть на счет в банке по 25,000 каждый год 1 января. Первый платеж принесет нам проценты за 5 лет, второй — за 4 года, третий — за 3 года, четвертый — за 2 год и, наконец, платеж, сделанный в начале пятого года, принесет нам проценты за один год. Коэффициенты наращения я взяла из соответствующей таблицы, которую можно открыть по ссылке.
25,000*1,6105+25,000*1,4641 +25,000*1,3310 + 25,000*1,2100 + 25,000*1,1000 = 25,000* (1,6105+1,4641+1,3310+1,2100+1,1000) = 25,000*6,7156 = 167,890
Таким образом, если начинать вносить 25,000 каждый год в начале годового периода и делать это в течение 5 лет, то через 5 лет сумма на счете будет равна $167,890. Этот вариант В выгодней, чем варианты А и Б, которые были рассмотрены раньше.
- Вариант А — $100,000, внесенные сегодня, накопят на банковском счете через 5 лет только 161,050
- Вариант Б — $25,000, внесенные на счет в конце каждого из 5 последующих лет, накопят через 5 лет только $152,628
Как видно из двух последних примеров, большое значение имеет момент, когда производятся платежи: в начале или в конце периода. Поэтому, если нужно рассчитать дисконтированную или будущую стоимость любых денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.
Как эти расчеты могут пригодиться в жизни?
В примерах выше были разобраны абстрактные примеры аннуитетов. Но с аннуитетными денежными потоками мы встречаемся и в реальной жизни. Например, интересно будет рассчитать, сколько удастся накопить на сберегательном счете, если откладывать каждый месяц часть зарплаты. Подобным же образом можно будет рассчитать, скажем, дисконтированную стоимость всех платежей по автокредиту. Выплаты банку при покупке автомобиля (и не только автомобиля) в кредит представляют собой аннуитет. Его дисконтированная (приведенная к сегодняшнему дню) стоимость — это и будет стоимость приобретаемого автомобиля. Можно точно узнать, сколько вы переплачиваете при покупке машины в кредит в сравнении с вариантом покупки с уплатой полной суммы сразу. А также можно будет сравнить кредитные предложения разных банков. Единственная проблема в таких расчетах – выбрать правильную месячную ставку дисконтирования.
Вечная рента
Вечная рента — это аннуитет, платежи которого продолжаются в течение неограниченного срока. Другими словами – это серия одинаковых платежей, которая продолжается вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.
В викторианскую эпоху все английские аристократы жили на проценты со своего капитала. Чем больший капитал лежал в банке, тем большие средства можно было потратить на жизнь и при этом не работать. Капитал переходил по наследству, и теоретически (если бы не было банкротств банков, войн и инфляции) так могло бы продолжаться вечно.
Будущая стоимость вечной ренты не имеет смысла, так как платежи продолжаются неограниченно долго. Однако текущая стоимость вечной ренты является конечной суммой, которую можно вычислить по формуле:
PV = платеж/R,
где R – это банковская ставка %, PV — текущая стоимость
Например, если хочется снимать со счета проценты в сумме 500,000 рублей в год, а годовая банковская ставка составляет 8%, то это значит, что сумма вклада на банковском счете должна быть равна:
500,000/0,08 = 6,250,000 рублей (PV).
В этом случае (если у банка не отберут лицензию или банк не обанкротится сам) можно снимать такие проценты постоянно на протяжении неограниченного периода времени. Единственное, что может нарушить такую идиллическую картину, — это инфляция, благодаря которой деньги обецениваются. Поэтому с течением времени снимаемые проценты будут приносить всё меньше материальных благ.
Философское отступление для тех, кто дочитал до этого места.
Чтобы рента была вечной, нужно сохранять капитал, с которого мы получаем эту ренту. Этот закон действует не только в финансовом мире. Человечество живет за счет природной ренты – оно пользуется ресурсами планеты, которые, к сожалению, исчерпаемы. Если брать от природы слишком много, природная рента иссякнет. Истощение земных ресурсов происходит на наших глазах.
При традиционном рыболовстве рыбу ловили понемногу, но это могло продолжаться вечно. Индустриальные города требуют рыбу определенного сорта и качества, для вылова которой применяется промышленный рыболовный флот. Крупные суда гонятся лишь за прибылью и не уважают океан. В настоящее время 80% мест промысловых районов Европы истощены. По расчетам ученых к 2050 году промышленное рыболовство сойдет на нет. Рыбная «рента» исчерпает себя. Много ли других ресурсов останется у человечества через 35-50 лет?
«Мир достаточно велик, чтобы удовлетворить нужды любого человека, но слишком мал, чтобы удовлетворить человеческую жадность» Махатма Ганди
Планета Земля – это наш единственный дом. Думаем ли мы об этом?
Вы можете почитать другие статьи по данной теме:
2. Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно
Рассчитать свой потенциальный доход по вкладу можно самостоятельно, не полагаясь на калькуляторы дохода, которые размещены на сайтах банковских учреждений. В этой статье на конкретных примерах показано, как рассчитать доход по вкладу с капитализацией процентов (ежеквартальной, ежемесячной, ежедневной, непрерывной) и как рассчитать эффективную ставку по вкладам с капитализацией.




Большое спасибо. Самое понятное объяснение. Это будет моя настольная статья.
Спасибо за такие статьи 🙂
просто и доступно,благодарю
Спасибо за доступное объяснение, в вот на лекциях в институте ничего не поняла.
Обычно не оставляю комментарии! Но здесь невозможно этого не сделать — большое человеческое спасибо за такие понятные и ценные знания!
Спасибо большое, есть только маленькое замечание во второй задаче ошибка в решении:
25,000*1,4641 + 25,000*1,3310 +25,000*1,2100 +25,000*1,1000 + 1 = 152,628
И как должно быть:
25,000*1,4641 + 25,000*1,3310 +25,000*1,2100 +25,000*1,1000 + 25000 = 152,628
Большое спасибо, что указали на ошибку. Исправила.
Спасибо большое за такое доступное объяснение! Очень жду новых статей.
В инсте проходим сейчас финансовый менеджмент, ничего не понимал сидя на лекциях, аж страшно стало, что я глупый…нашел Ваши статьи, примеры и чувствую себя образованным теперь) спасибо за простоту изложения, разжованность, интересные примеры и философские отступления)
теперь уверен, что сдам зачет в субботу)
Спасибо и Вам за комментарий. Обратная связь очень важна, потому что иначе как я узнаю, насколько понятным получился текст. На лекциях обычно преподаватели слишком быстро начитывают материал, поэтому теряется смысловая нить. Лучше всего читать учебники перед лекцией, и задавать вопросы преподавателю в процессе объяснения. Ведь преподаватель для того и нужен, чтобы объяснить непонятное. А не для того, чтобы дублировать учебник.
Спасибо огромное! Хотелось бы, что бы больше статьей по финансовым вопросам, а именно финансовому моделированию публиковалось!
Спасибо за очень доступные объяснения.
Хотелось бы обратить Ваше внимание на опечатку: коэффициент дисконтирования аннуитета должен выглядеть следующим образом: 1/R — 1/(R*(1+R)^n)
Алексей, спасибо за замечание. Как это я так написала. Главное, ведь статья давно написана, никто до Вас не заметил.
спасибо большое очень понятно и доступно
{qoute}Таким образом, если начинать вносить 25,000 каждый год в начале годового периода и делать это в течение 5 лет, то через 5 лет сумма на счете будет равна $167,890. Этот вариант В выгодней, чем варианты А и Б, которые были рассмотрены раньше.{/quote}
т.е. 125000<100000, странный вывод
А подумать лень? И, наверное, лень вдумчиво прочитать, что действительно написано?
167,890 > 161,050 (вариант А) > 152,628 (Вариант Б)
Вариант А — $161,050
Вариант Б — $152,628
Вы, вроде как взяли цифры из разных пунктов. Вносить в начале года — это из наращивания, а вывод — это из дисконтирования.
А ведь действительно просто, спасибо. Прямо захотелось учиться. Буду.
Спасибо!
Спасибо огромное за статью. В статье объясняются сложные понятия простым и доступным языком. Кроме того, текст содержит и математические понятия и философские размышления. Точная наука и гуманитарная идут нога в ногу. Но математика — царица!!! Класс!!!
Спасибо огромное за такие доступные статьи. Очень мне помогли понять содержание норвежских учебников по финансированию и инвестированию и содержание лекций прочитанный лектором — норвежцем. Сейчас можно смело читать норвежский учебник и наложить норвежские термины на полученную здесь информацию. Отлично, кратко и доступно. А также методика подготовки к экзамену очень актуальна.
Спасибо за помощь и ваш труд!Материал отличный
Момент: В примере 1 На рисунке ставка дисконтирования для 2 года 0,8464, в таблице и расчетах 0,8264.
Инна, да спасибо, надо переделать рисунок
Отлично!!!
Спасибо автору за подробное и доступное объяснение! Автор объясняет как сказку сказывает))
Благодарю Вас за замечательную статью, написанную доступным языком!Читать приятно и интересно.Никогда не думала, что финансовый менеджмент — это так увлекательно!
1-й год 25000 ,2-ой уже 50000 И так далее ,75000,100000 Сумма каждый год увеличивается на 25.000?или я ничего не понимаю?
Спасибо за объяснение, более понятного в интернете не нашёл.
Огромное спасибо, прекрасная цитата приведена в конце статьи. Пусть в людях пробудится любовь и осознанность..
Спасибо за статью, очень познавательно. Но меня все таки мучает, один вопросик: почему в примере А сумма для расчетов берется = 100.000 $, а в примере Б = 125.000 $ (5 лет по 25.000$)???