Понятие, формула дисконтирования. Таблица дисконтирования — как ей пользоваться для расчета дисконтированной стоимости
 Знаете ли вы, что означает дисконтирование? Если вы читаете эту статью, значит, вы уже слышали это слово. И если вы пока не поняли до конца, что это такое, то эта статья для вас. Даже если вы не собираетесь сдавать экзамен Дипифр, а просто хотите разобраться в этом вопросе, прочитав эту статью, вы сможете прояснить для себя понятие дисконтирования.
Знаете ли вы, что означает дисконтирование? Если вы читаете эту статью, значит, вы уже слышали это слово. И если вы пока не поняли до конца, что это такое, то эта статья для вас. Даже если вы не собираетесь сдавать экзамен Дипифр, а просто хотите разобраться в этом вопросе, прочитав эту статью, вы сможете прояснить для себя понятие дисконтирования.
Данная статья доступным языком рассказывает о том, что такое дисконтирование. На простых примерах в ней показана техника расчета дисконтированной стоимости. Вы узнаете, что такое фактор дисконтирования и научитесь пользоваться таблицами коэффициентов дисконтирования.
Понятие и формула дисконтирования доступным языком
Чтобы проще было объяснить понятие дисконтирования, начнём с другого конца. А точнее, возьмем пример из жизни, знакомый каждому.
Пример 1. Представьте, что вы пришли в банк и решили сделать вклад в размере 1000 долларов. Ваши 1000 долларов, положенные в банк сегодня, при банковской ставке 10% будут стоить 1100 долларов завтра: нынешние 1000 долларов + проценты по вкладу 100 (=1000*10%). Итого через год вы сможете снять 1100 долларов. Если выразить этот результат через простую математическую формулу, то получим: $1000*(1+10%) или $1000*(1,10) = $1100.
Через два года нынешние 1000 долларов превратятся в $1210 ($1000 плюс проценты за первый год $100 плюс проценты за второй год $110=1100*10%). Общая формула приращения вклада за два года: (1000*1,10)*1,10 = 1210
С течением времени величина вклада будет расти и дальше. Чтобы узнать, какая сумма вам причитается от банка через год, два и т.д., надо сумму вклада умножить на множитель: (1+R)n
- где R – ставка процента, выраженная в долях от единицы (10% = 0,1)
- N – число лет
В данном примере 1000*(1,10)2 = 1210. Из формулы очевидно (да и из жизни тоже), что сумма вклада через два года зависит от банковской ставки процента. Чем она больше, тем быстрее растет вклад. Если бы ставка банковского процента была другой, например, 12%, то через два года вы бы смогли снять с вклада примерно 1250 долларов, а если считать более точно 1000*(1,12)2 = 1254.4
Таким способом можно рассчитать величину вашего вклада в любой момент времени в будущем. Расчет будущей стоимости денег в английском языке называется «compounding». Данный термин на русский язык переводят как «наращение» или калькой с английского как «компаундирование». Лично мне больше нравится перевод данного слова как «приращение» или «прирост».
Смысл понятен – с течением времени денежный вклад увеличивается за счет приращения (прироста) ежегодными процентами. На этом, собственно говоря, построена вся банковская система современной (капиталистической) модели мироустройства, в которой время – это деньги.
Теперь давайте посмотрим на данный пример с другого конца. Допустим, вам нужно отдать долг своему приятелю, а именно: через два года заплатить ему $1210. Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года — эквивалентны друг другу. Не важно, что выберет ваш приятель – это две равноценные возможности.
ПРИМЕР 2. Допустим, через два года вам надо сделать платёж в сумме $1500. Чему эта сумма будет равноценна сегодня?
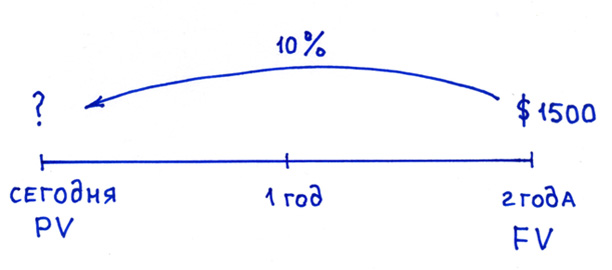
Чтобы рассчитать сегодняшнюю стоимость, нужно идти от обратного: 1500 долларов разделить на (1,10)2 , что будет равно примерно 1240 долларам. Этот процесс и называется дисконтированием.
Если говорить простым языком, то дисконтирование – это определение сегодняшней стоимости будущей денежной суммы (или если говорить более правильно, будущего денежного потока).
Если вы хотите выяснить, сколько будет стоить сегодня сумма денег, которую вы или получите, или планируете потратить в будущем, то вам надо продисконтировать эту будущую сумму по заданной ставке процента. Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
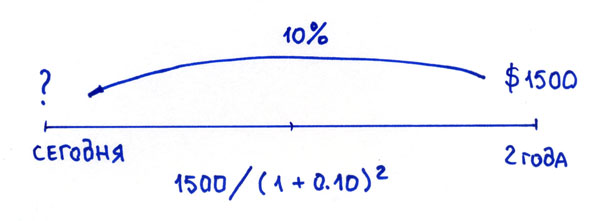
Когда мы дисконтируем — мы идём от будущего к сегодняшнему дню.
Дисконтирование
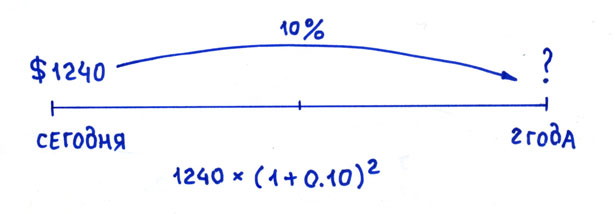
Когда мы наращиваем — мы идём от сегодняшнего дня в будущее.
Наращение
Формула для расчета дисконтированной стоимости или формула дисконтирования для данного примера имеет вид: 1500 * 1/(1+R)n = 1240.
Математическая формула дисконтирования в общем случае будет такая: FV * 1/(1+R)n = PV. Обычно её записывают в таком виде:
PV = FV * 1/(1+R)n
Коэффициент, на который умножается будущая стоимость 1/(1+R)n называется фактором дисконтирования от английского слова factor в значении «коэффициент, множитель».
В данной формуле дисконтирования: R – ставка процента, N – число лет от даты в будущем до текущего момента.
Таким образом:
- Compounding или Приращение – это, когда вы идете от сегодняшней даты в будущее.
- Discounting или Дисконтирование – это, когда вы идете из будущего к сегодняшнему дню.
Обе «процедуры» позволяют учесть эффект изменения стоимости денег с течением времени.
Конечно, все эти математические формулы сразу наводят тоску на обычного человека, но главное, запомнить суть. Дисконтирование – это когда вы хотите узнать сегодняшнюю стоимость будущей суммы денег (которую вам надо будет потратить или получить).
Надеюсь, что теперь, услышав фразу «понятие дисконтирования», вы сможете объяснить любому, что подразумевается под этим термином.
Приведенная стоимость – это дисконтированная стоимость?
В предыдущем разделе мы выяснили, что
Дисконтирование– это определение текущей стоимости будущих денежных потоков.
Не правда ли, в слове «дисконтирование» слышится слово «дисконт» или по-русски скидка? И действительно, если посмотреть на этимологию слова discount, то уже в 17 веке оно использовалось в значении «deduction for early payment», что означает «скидка за раннюю оплату». Уже тогда много лет назад люди учитывали временную стоимость денег. Таким образом, можно дать еще одно определение: дисконтирование – это расчет скидки за быструю оплату счетов. Эта «скидка» и является мерилом временной стоимости денег или time value of money.
Дисконтированная стоимость – это текущая стоимость будущего денежного потока (т.е. будущий платеж за вычетом «скидки» за быструю оплату). Ее еще называют приведенной стоимостью, от глагола «приводить». Говоря простыми словами, приведенная стоимость – это будущая денежная сумма, приведенная к текущему моменту.
Если быть точным, то дисконтированная и приведенная стоимость – это не абсолютные синонимы. Потому что приводить можно не только будущую стоимость к текущему моменту, но и текущую стоимость к какому-то моменту в будущем. Например, в самом первом примере можно сказать, что 1000 долларов, приведенные к будущему моменту (через два года) при ставке 10% равны 1210 долларов. То есть, я хочу сказать, что приведенная стоимость – это более широкое понятие, чем дисконтированная стоимость.
Кстати, в английском языке такого термина (приведенная стоимость) нет. Это наше, чисто русское изобретение. В английском языке есть термин present value (текущая стоимость) и discounted cash flows (дисконтированные денежные потоки). А у нас есть термин приведенная стоимость, и он чаще всего используется именно в значении «дисконтированная» стоимость.
Таблица дисконтирования
Чуть выше я уже приводила формулу дисконтирования PV = FV * 1/(1+R)n, которую можно описать словами как:
Дисконтированная стоимость равна будущая стоимость, умноженная на некий множитель, который называется фактором дисконтирования.
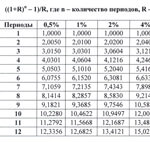
Коэффициент дисконтирования 1/(1+R)n, как видно из самой формулы, зависит от ставки процента и количества периодов времени. Чтобы не вычислять его каждый раз по формуле дисконтирования, пользуются таблицей, показывающей значения коэффициента в зависимости от % ставки и количества периодов времени. Иногда она называется «таблица дисконтирования», хотя это не совсем правильный термин. Это таблица коэффициентов дисконтирования, которые рассчитываются, как правило, с точностью до четвертого знака после запятой.
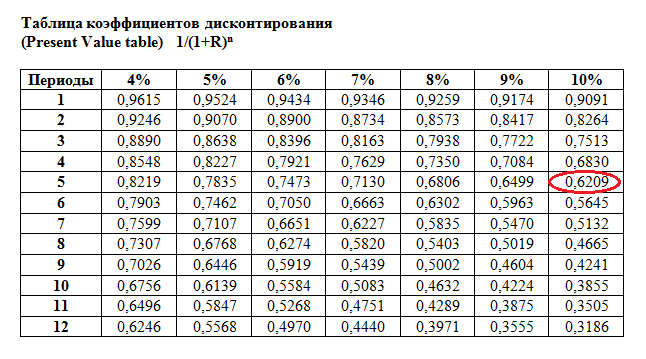
Пользоваться данной таблицей коэффициентов дисконтирования очень просто: если вы знаете ставку дисконтирования и число периодов, например, 10% и 5 лет, то на пересечении соответствующих столбцов находится нужный вам коэффициент.
Пример 3. Давайте разберем простой пример. Допустим, вам нужно выбрать между двумя вариантами:
- А) получить 100,000 долларов сегодня
- Б) или 150,000 долларов одной суммой ровно через 5 лет
Что выбрать?
Если вы знаете, что банковская ставка по 5-летним депозитам составляет 10%, то вы легко можете посчитать, чему равна сумма 150,000 долларов к получению через 5 лет, приведенная к текущему моменту.
Соответствующий коэффициент дисконтирования в таблице равен 0,6209 (ячейка на пересечении строки 5 лет и столбца 10%). 0,6209 означает, что 62,09 цента, полученные сегодня, равны 1 доллару к получению через 5 лет (при ставке 10%). Простая пропорция:
|
сегодня |
через 5 лет |
|
62,09 цента |
$1 |
|
X? |
150,000 |
Таким образом, $150,000*0,6209 = 93,135.
93,135 — это дисконтированная (приведенная) стоимость суммы $150,000 к получению через 5 лет.
Она меньше, чем 100,000 долларов сегодня. В данном случае, синица в руках действительно лучше, чем журавль в небе. Если мы возьмем 100,000 долларов сегодня, положим их на депозит в банке по 10% годовых, то через 5 лет мы получим: 100,000*1,10*1,10*1,10*1,10*1,10 = 100,000*(1,10)5 = 161,050 долларов. Это более выгодный вариант.
Чтобы упростить это вычисление (вычисление будущей стоимости при заданной сегодняшней стоимости), можно также воспользоваться таблицей коэффициентов. По аналогии с таблицей дисконтирования эту таблицу можно назвать таблицей коэффициентов приращения (наращения). Вы можете построить такую таблицу самостоятельно в Excele, если используете формулу для расчета коэффициента приращения:(1+R)n .
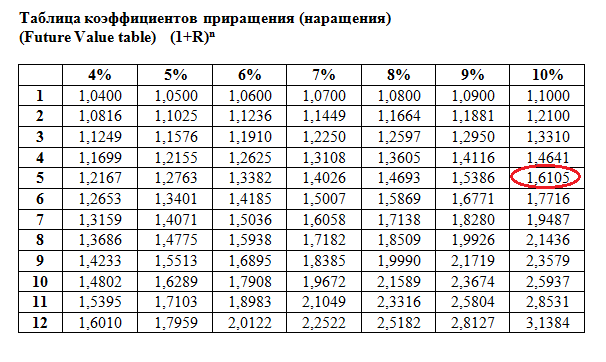 Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
С помощью такой таблицы легко будет посчитать, сколько денег нужно положить в банк сегодня, если вы хотите получить определенную сумму в будущем (не пополняя вклад). Чуть более сложная ситуация возникает, когда вы хотите не только положить деньги на депозит сегодня, но и собираетесь каждый год добавлять определенную сумму к своему вкладу. Как это рассчитать, читайте в следующей статье. Она называется формула аннуитета.
Философское отступление для тех, кто дочитал до этого места
Дисконтирование базируется на знаменитом постулате «время — деньги». Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Всё, что нам нужно – это решиться: посадить дерево, начать свое дело, стать на путь, ведущий к исполнению мечты. Чем раньше мы начнем действовать, тем больший урожай мы получим в конце пути. Нужно превращать время, отпущенное нам в нашей жизни, в результаты.
«Семена цветов, которые распустятся завтра, сажают сегодня». Так говорят китайцы.
Если вы мечтаете о чем-то, не слушайте тех, кто вас отговаривает или подвергает сомнению ваш будущий успех. Не ждите удачного стечения обстоятельств, начинайте как можно раньше. Превращайте время вашей жизни в результаты.
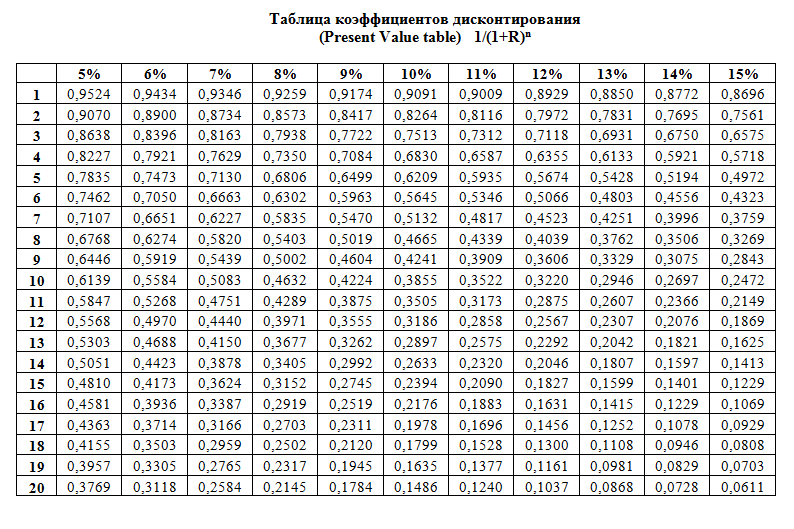
Большая таблица коэффициентов дисконтирования (открывается в новом окне):
Вы можете прочитать другие статьи по теме Финансы:
1. Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Рассчитать свой потенциальный доход по вкладу можно самостоятельно, не полагаясь на калькуляторы дохода, которые размещены на сайтах банковских учреждений. В этой статье на конкретных примерах показано, как рассчитать доход по вкладу с капитализацией процентов (ежеквартальной, ежемесячной) и как рассчитать эффективную ставку по вкладам с капитализацией.
2. Формула аннуитета. Вечная рента. Это надо знать каждому! (не для банкиров)
Вечная рента — это серия одинаковых платежей, которые продолжаются вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.
3. Формула расчета NPV инвестиционного проекта. Это просто.
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
4. Внутренняя норма доходности. Формула расчета IRR инвестиционного проекта
В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя (в Excel, графический) и интерпретации полученных результатов. Два примера из жизни, с которыми сталкивается каждый человек
5. Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала.
По своей сути ставка дисконтирования при анализе инвестиционных проектов — это ставка процента, по которой инвестор привлекает финансирование. Как ее рассчитать?
Самые интересные статьи по теме МСФО и Дипифр:






СПАСИБО АВТОРУ !!! ЗАМЕЧАТЕЛЬНО , А ГЛАВНОЕ ОЧЕН ВНЯТНО ВСЕ ПРЕДСТАВЛЕНО !!!
Прекрасная статья. Полезная и красиво подана.
Спасибо за очень понятное объяснение! Сдавала дипифр 5 лет назад и все забыла. Но тут так все разложено, что уже не забуду)
ОГРОМНОЕ СПАСИБО! СЛОЖНОЕ ИЗЛОЖЕНО ДОХОДЧИВО И С ЛЮБОВЬЮ
Спасибо большое! На простом и понятном языке объяснили технарю всю эту жуткую экономику)
более доходчивого разъяснения не нашел!спасибо
Спасибо, на лекциях не поняла, а тут все понятно!
Большое спасибо! Очень доступно, понятно и кратко!
Умничка, все грамотно изложено, побольше бы таких авторских статей
я тоже прочитал, кажется понял, особенно понравилось про *Философское отступление*
Огромное спасибо! У вас талант объяснять. На первый взгляд сложные вещи становится простыми и доступными.
Спасибо за доступное изложение материала, ничего лишнего.
Согласен с предыдущим комментарием — у Вас талант!
С уважением.
Спасибо всем за добрые слова! Это вдохновляет на написание новых статей. Честно говоря, не ожидала, что статья про дисконтирование будет настолько популярной, и будет нравиться людям. Тем приятнее, что это так.
Спасибо большое! Действительно очень доходчиво объяснили даже таким тугодумам как я)
Я бы хотел присоединиться к выраженным благодарностям в адрес автора статьи! Очень доходчиво.
Спасибо Автору за статью. Очень все доходчиво написано и разъяснено. С удовольствием дочитала до конца. Спасибо большое.
Очень доступно и подробно написано, спасибо огромное, что помогли разобраться в этой не простой теме для технаря.
Благодарю Автора за столь доступное описание. Молодчина, все понятно и доходчиво.
спасибо, понятно доступно, благодарю автора, все бытак.
Завалил экзамен по управлению проектом, потому что не понял что такое дисконтирование! Прочитал статью и все понял! Спасибо! Завтра иду на пересдачу, надеюсь сдам)
Спасибо большое, уважаемый автор.
Вы удивительно доступно и, в то же время, достаточно коротко изложили материал, передав в статье суть и природу дисконтирования, затронув, на мой взгляд, все базовые вопросы.
Огромное спасибо за доходчивое объяснение материала!
Даже в университете не так доходчиво объясняют. Сдала госы (учусь на заочном отделении) благодаря вашим статьям! Спасибо вам!
Спасибо большое за очень доходчивое объяснение!
всё стало понятно, спасибо от души!!!
Спасибо автору, все так просто и понятно.
Благодарю за статью, теперь буду частым гостем на вашем сайте!
Спасибо огромное за такое доступное изложение данной темы. С уважением, Елена
Огромное спасибо! Приятно читать
спасибо большое! Статья просто блеск. Очень красиво и понятно написано.
Необходимо отметить, что в этих формулах время измеряется в единицах периода ставки дисконтирования
Спасибо за Ваш труд.
Выражаю Вам огромную благодарность за разъяснение для меня этой темы. Написано ясно, просто и доходчиво!!! Жду новых статей по финансовой граммотности. Хотелось бы знать, есть ли еще статьи, написанные Вами.
Спасибо огромное! Объяснили доходчиво и, главное, интересно! Сохранила Ваш сайт в закладках
Автору огромнейшее спасибо!!! Все досконально разжёвано, что конечно же, в разы упрощает усвоение темы методов оценки экономической эффективности инвестиций.
Большущее спасибо автору! невероятная статья! Полгода билась с финансовым менеджментом, пока не нашла этот сайт
Уважаемый автор! У Вас талант просто объяснять сложное. Надеюсь, Вы преподаете в ВШЭ.
Милая автор. Вы и ваша статья прекрасны.
Автору велике дякую!
Отличная статья! Респект. Спасибо автору. Все просто, доступно и с философским хорошим смыслом в конце 🙂
Огонь!
Спасибо! Все очень доступно написано! Читается легко и с пониманием!
Сразу видно чть совестливый человек
Спасибо Огромное!!
Огромное спасибо, очень познавательно)))
И от меня спасибо за то, что помогаете другим людям! Удачи Вам и всего наилучшего!
Пипец!!! А я голову ломал при написании бизнес-плана. Оказывается все просто. Спасибо. Очень доходчиво и интересно читать.
SPASIBOOOOOO
Спасибо автору статьи большое! Так понятно объяснено! Это невероятно важно — уметь объяснять, тем более на тексте. Не каждый это может, спасибо.
Спасибо. Понятнее, чем на MBA
Спасибо за четкое и понятное изложение материала.
Особенно ярко видно как действует расчет на реальных примерах.
За философское отступление благодарю в частности.)
Всех благ!
Замечательная статья! Браво автору!
Спасибо огромное Автору этой статьи. Очень понятно и расширенно объясняет!
Спасибо огромное! очень доступно! буду частенько пользоваться вашими статьями! успехов) Читатель с Казахстана)
Автору огромнейшее спасибо, освежил знания за 5 минут! Успехов Вам, если у Вас на сайте есть подписка на рассылку — включите меня, пожалуйста, в неё!
Нашёл подписку, подписался!)
Огромное спасибо за статью. Все понятно, а главное с примерами!
Хотелось бы уточнить: если мы кладем 1 доллар при ставке 10%, то через 5 лет у нас будет 1,6105 доллар за счет банковских процентов. Но в то же время, если мы приведем данную сумму к текущей стоимости, предположив что инфляция будет сжирать 10% (коэффициент 0,6209), то получим тот же 1 доллар?
Получается, ожидая определенный уровень инфляции мы можем понять какой банковский (или проектный) процент нам необходим, чтобы 1) не потерять (обесценить) имеющие накопления и 2) прирастить к накоплениям еще хоть что-нибудь.
Просто супер, спасибо автору за элементарное объяснение, сколько прослушала и прочитала, но только сейчас поняла толк в дисконте. Спасибо
Огонь!
Просто здорово! Все разложилось по полочкам! Автор молодец!
Спасибо! Действительно очень доходчиво. И очень актуально для бухгалтера в связи со стремлением нашего замечательного ЦБ привести РСБУ к МСФО.
Огромное спасибо! Наконец-то дошло!
Спасибо огромное, отличная статья, по полочкам все разложилось, очень понятно. Искреннее спасибо таким авторам!!
Спасибо большое автору!)
Очень доходчивое обьяснение, благодарю.
Огромное спасибо! Автор молодец!
Прекрасно и доходчиво изложено. Поймут все, кто хочет понять. Спасибо автору.
Подскажите ежемесячный расчет дисконтирования отличается от годового?
Вроде бы все понял, но кроме расчета доходности депозита, где может пригодится расчет дисконтированной стоимости? Пару бы практических примеров..
Спасибо.
Философская часть о том, что надо сейчас тратить деньги и сажать яблоню противоречит сути дисконтирования и всей статье, а именно — отодвинуть траты на будущее. Готов к полемике с автором более подробно.
Здравствуйте!
Подскажите, как расчитать NPV, если ожидаемые доходы организации в задаче в кварталах?При ставке дисконтирования в 16%?
везде сложно о простом ,тут просто о простом .
++++++++++++++++++++++++++++++++++++ спасибо
Огромная благодарность за статью !
Большое спасибо за статью!
Все просто и понятно изложено, очень интересно и легко прочиталось!
Спасибо огромное за такое понятливое разъяснение!!!
Здравствуйте, хочу понять, насколько выгодно инвестору следующий расклад:
Первый инвестор считает:
Годовой процент доходности. Срок службы данного источника тепла составляет минимум 25 лет. Сумма вложений 55 277 евро сегодня. Прибыль за 25 лет составит 147 578 евро.
Считает процент доходности в год по формуле:
Доходность = Прибыль/сумма вложений * 1 год/25 лет * 100%.
Теперь подставляем данные в формулу: (147 578/54 197) * (1/25) * 100% и получаем 10,89% доходности в год.
Первый инвестор считает выгодно!
Второй инвестор считает:
Дисконтирование – это определение сегодняшней стоимости будущей денежной суммы (или если говорить более правильно, будущего денежного потока). Если вы хотите выяснить, сколько будет стоить сегодня сумма денег, которую вы или получите, или планируете потратить в будущем, то вам надо про дисконтировать эту будущую сумму по заданной ставке процента. Эта ставка называется «ставкой дисконтирования».
В нашем случае ставка дисконтирования равна 4% — это инфляция и больше ничего. Когда мы дисконтируем — мы идём от будущего к сегодняшнему дню, по формуле:
PV = FV * 1/(1+R)n где,
PV – это текущая стоимость, она нам сейчас нам не известна.
FV это будущая прибыль -147 578 евро.
R – ставка инфляции,
n – степень — число лет от даты в будущем до текущего момента.
Подставляем наши данные в данную формулу и производим расчёты:
PV = 147 578 * 1 / (1 + 4%) 25 =
PV = 147578 * 1 / (1,04) 25 =
PV = 147 578 * 1 / 2,6658 =
PV = 147 578 * 0,37511 =
PV = 55 358,98 евро.
Сумма вложений: 54 197
Второй инвестор считает, почти по нулям. Не выгодно!
Выгодно это инвесторам или нет? Получается один инвестор считает годовой процент доходности, а другой считает согласно дисконтности. Кто из инвесторов прав?
Какой Вы замечательный!!!!!Вчера случайно «нарвалась» на Вашу статью -нет слов, нет лайков да и не хватит.Спасибо очень-очень огромное.
Огромное спасибо автору за информацию разложенную по полочкам! Шесть лет с момента написания, а статья актуальна. Уверен что данное творение и дальше будет пользоваться интересом и люди нашедшие эту статью так же как и я остановятся на поисках. Автору желаю развития и творческих успехов.
Действительно очень доступно, спасибо
Спасибо огромное автору статьи !!!! Так легко ,просто, понятно никто не мог мне объяснить про дисконтирование. После вашей статьи все стало по полочкам-ЯСНО, как дважды два. Уверена, что эта статья поможет еще многим . Автору желаю больших успехов.
Большое спасибо автору! Очень интересно чиать, все понятно, четко и по делу.
Безмерно благодарна и выражаю свое восхищение!
Спасибо автору. Действительно у него талант разжёвывать информацию и раскладывать все по полочкам.
Огромное спасибо автору!!! Прекрасное раскрытие темы, которая никак не укладывалась в моей голове. Буду читать следующие статьи.
Прекрасное раскрытие темы! У автора настоящий талант, я Вам очень благодарна!
Спасибо большое, доступно и понятно.
Изумительная статья! Просто, доходчиво и по делу. Пока разбиралась в теме наткнулась на множество других ресурсов, где информация подаётся скомкано и в слишком сложной форме. Как чудесно, что есть люди, которые создают вещи, чтобы действительно помочь другим людям, а не просто чтобы написать. Спасибо!
Автору респект! Ваш труд остаётся актуален годами. Если бы преподаватели экономических вузов объясняли также доступно как вы, с экономикой и экономистами у нас бы был полный порядок.